Binary Tree Traversal Algorithms
Binary Trees are complex non-linear data structures that have wide-reaching uses. A common use case is a Binary Search Tree where data is arranged in a specific order and allows for very quick searching and sorting. This is mainly what we will be looking at today. Other uses could be in the implementation of a Heap data structure, or some compression algorithms.
Trees also relate to my previous post on renaming files in a directory. This is because directories lend themselves naturally to the structure of a tree. We used library functions to traverse a tree of files and rename them, but today we’ll be looking at how this traversal can be achieved manually.
There is a lot of recursion today which is one reason I wanted to cover this topic. Recursion can be quite difficult to follow but is an incredibly important tool for coding algorithms. I recommend reading up on it a little if you are new to it but I’ll try to explain things as I go!
Various methods of traversing binary trees Photo by Pearly85
Terminology
I think it would be useful to first cover the keywords and terminology used for discussing trees. The main concepts are:
- Tree: A graph that has no loops, ie. any two points are connected by exactly one path. - Rooted Tree: A tree where one node has been singled out as the ‘root’, ie. the starting point. - Leaf: A node that has no children.
- Internal Node: A node that has at least one child. - Height: The longest path from the root to a leaf.
Creating a Simple Binary Tree in Python
Python does not include an implementation of a tree by default. We could find a library to make one for us but that’s no fun!
To start with let’s just define the simplest starting point for a tree class.
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = NoneIt turns out this is enough code to build a full tree! We can now use this to manually build up each node by hand. For example, here is some code that produces a tree, and then under it I have made a graphical representation of that tree.
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = None
if __name__ == '__main__':
rootNode = Tree(50)
rootNode.leftChild = Tree(30)
rootNode.rightChild = Tree(70)
rootNode.leftChild.leftChild = Tree(20)
rootNode.leftChild.rightChild = Tree(40)
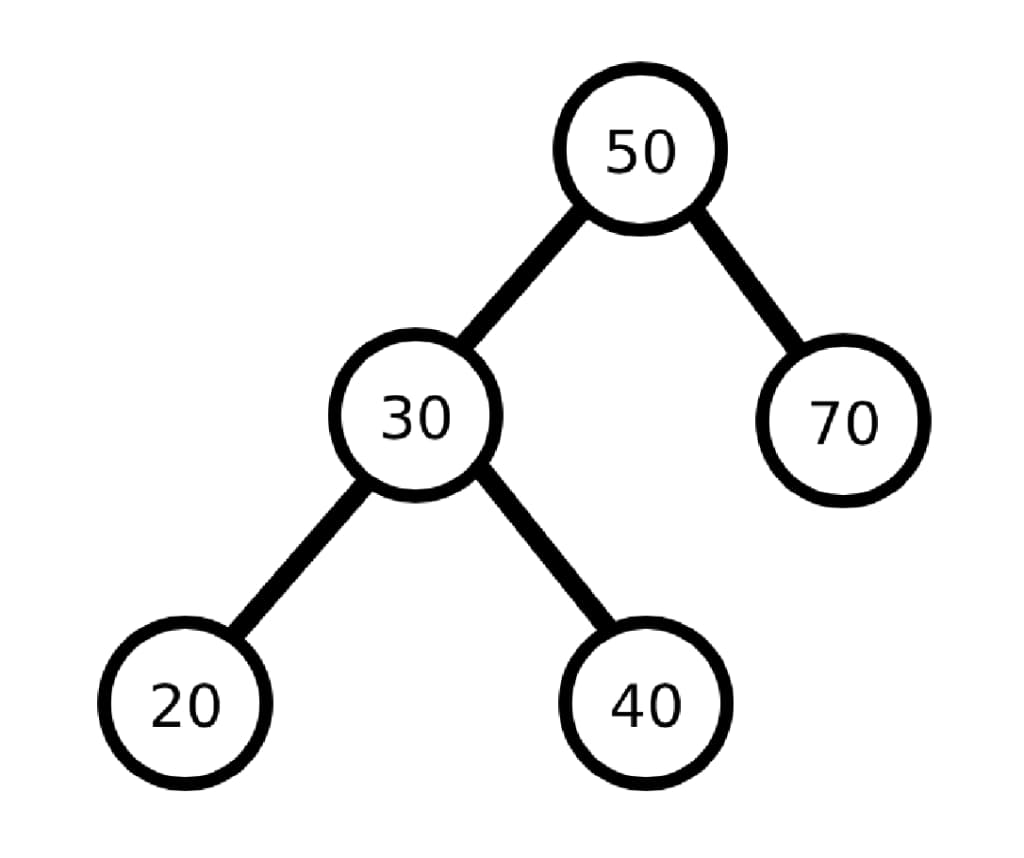
Well that was easy! However this is not a particularly useful way of building up trees because it requires us to manually enter which node is a child of which parent and thus it will get very messy very quickly. Instead, we can add a method to our ‘Tree’ class that takes a node’s value as input and positions it in the appropriate place in the tree. Since we are trying to make a binary search tree we have a couple of rules to satisfy when positioning a new node:
- Starting at the root, check if the new value is greater than or less than the root’s value. - If greater then move to the right child, if lesser then move the the left child. - Repeat this check on the child we moved to, moving left or right from there depending on size of the new node’s value compared to the child’s value. - Continue this process until we find an empty child on the correct side of a node.
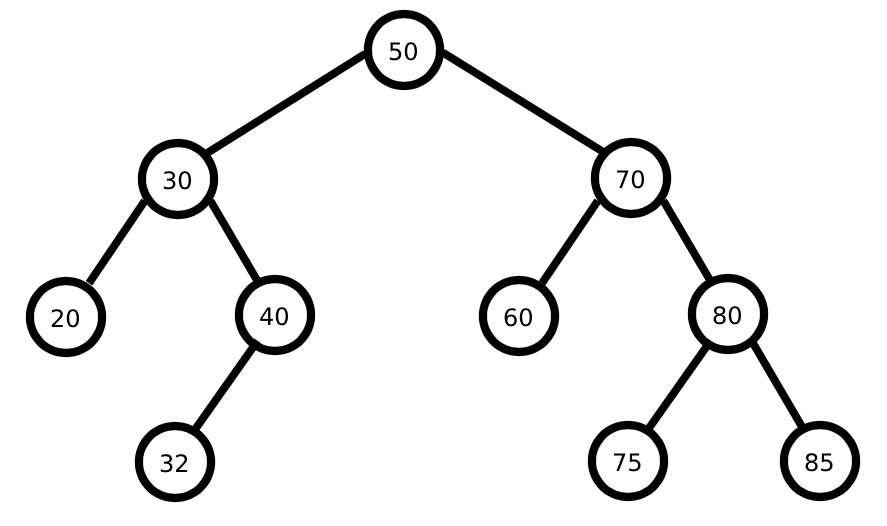
For example if I wanted to insert 32 into our tree above, we’d start at 50, move left to 30 (since 32 < 50), move right to 40 (since 32 > 30), and then position 32 as the left child of 40 (since 32 < 40 and this child is currently empty).
So here is an algorithm to implement this process automatically. Take note of the recursive calls.
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = None
def insertChild(self, node, value):
if node is None:
return Tree(value)
if value < node.value:
node.leftChild = self.insertChild(node.leftChild, value)
elif value > node.value:
node.rightChild = self.insertChild(node.rightChild, value)
return nodeSo (assuming we pass in the root node) we start at the top of the tree and do this greater/lesser check and traverse down the tree on the right/left side of the current node, respectively. We then re-call the function on the next node that we come to and it does exactly the same check. Eventually a node will have a child that has value ‘None’ and this will end our recursive calls and position our new node in that position.
So let’s build up a tree automatically!
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = None
def insertChild(self, node, value):
if node is None:
return Tree(value)
if value < node.value:
node.leftChild = self.insertChild(node.leftChild, value)
elif value > node.value:
node.rightChild = self.insertChild(node.rightChild, value)
return node
if __name__ == '__main__':
rootNode = Tree(50)
rootNode.insertChild(rootNode, 30)
rootNode.insertChild(rootNode, 20)
rootNode.insertChild(rootNode, 40)
rootNode.insertChild(rootNode, 32)
rootNode.insertChild(rootNode, 70)
rootNode.insertChild(rootNode, 60)
rootNode.insertChild(rootNode, 80)
rootNode.insertChild(rootNode, 75)
rootNode.insertChild(rootNode, 85)This will produce a tree that looks like this:
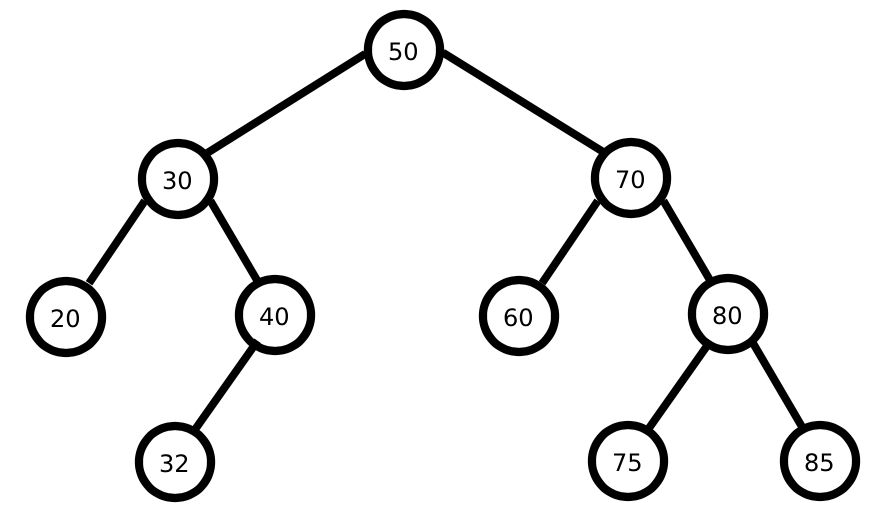
I’ve had to make this graphic by hand. Unfortunately there’s no nice way to view trees we create in Python (without using extra libraries), or even an easy way of printing the elements out. We need to code this ourselves so that we can actually check the tree we have created.
Trees are non-linear data structures so there is no single right way to traverse one. There are two main approaches we can take: depth-first or breadth-first traversal.
Depth-first will search all the way to the bottom of the tree first before working its way back up. It will then do the same thing on the next branch it finds. Breadth-first will visit every node on the current level of the tree, then every node on the next level down, and so on.
Let’s start by implementing a depth-first traversal.
Depth-First Tree Traversal
Strangely there are actually three standard subcategories of depth-first traversals: Pre-order, In-order, and Post-order. These describe the order at which we visit the three elements of each immediate subtree, ie. the root, the left node, and the right node. As a very quick overview we could summarise them as follows.
Given the subtree below…
Here is the order each traversal method would visit the nodes:
- Pre-Order: root -> left -> right - In-Order: left -> root -> right - Post-Order: left -> right -> root
This is useful information for coding each traversal but doesn’t help us understand them. Let’s look closer.
Visualising Depth-First Traversal
Imagine walking around the tree in an anti-clockwise loop, starting and ending at the root, and passing by every node. For the tree we built earlier, your path would look something like the grey line here:
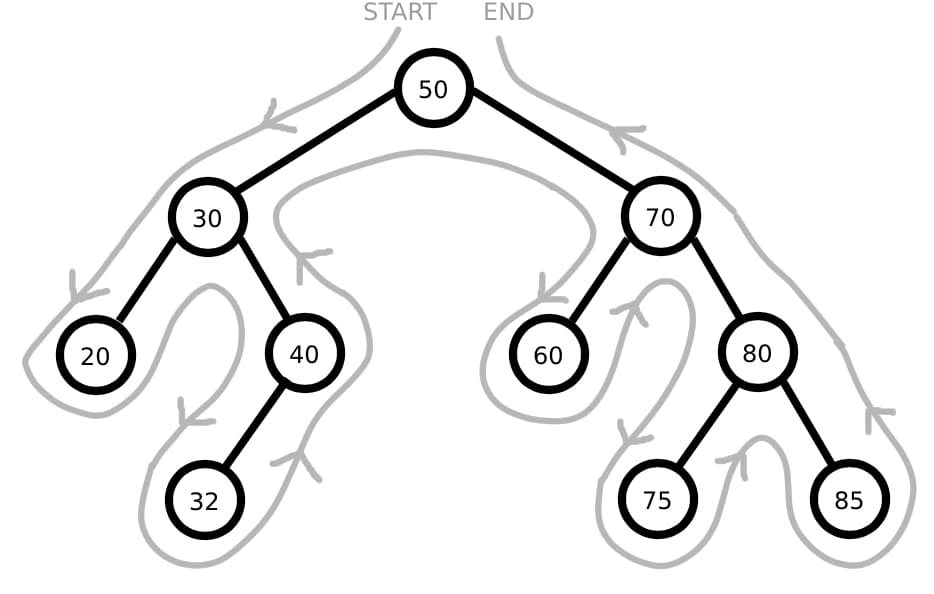
It turns out this is a really useful way of visualising how pre-order, in-order, and post-order visit each node. We do this by putting a spot to the left/bottom/right of each node, respectively, and noticing the order the grey line passes through these spots.
For pre-order traversal, the spot goes on the left of each node like so:
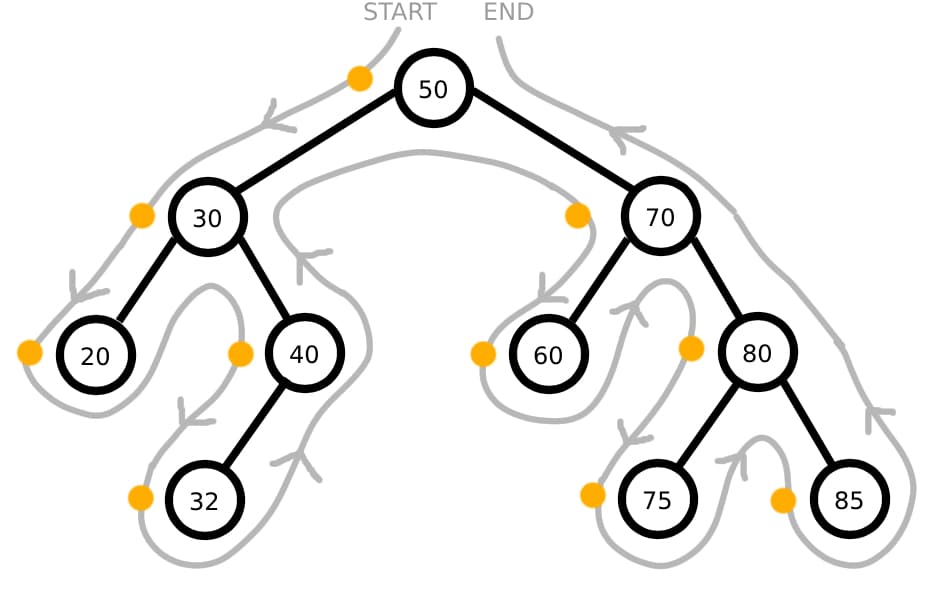
Tracking the order that the line passes through each node’s spot produces the following sequence: 50, 30, 20, 40, 32, 70, 60, 80, 75, 85. This is the pre-order traversal of the tree!
Similarly for in-order traversal, the spot goes on the bottom of each node:
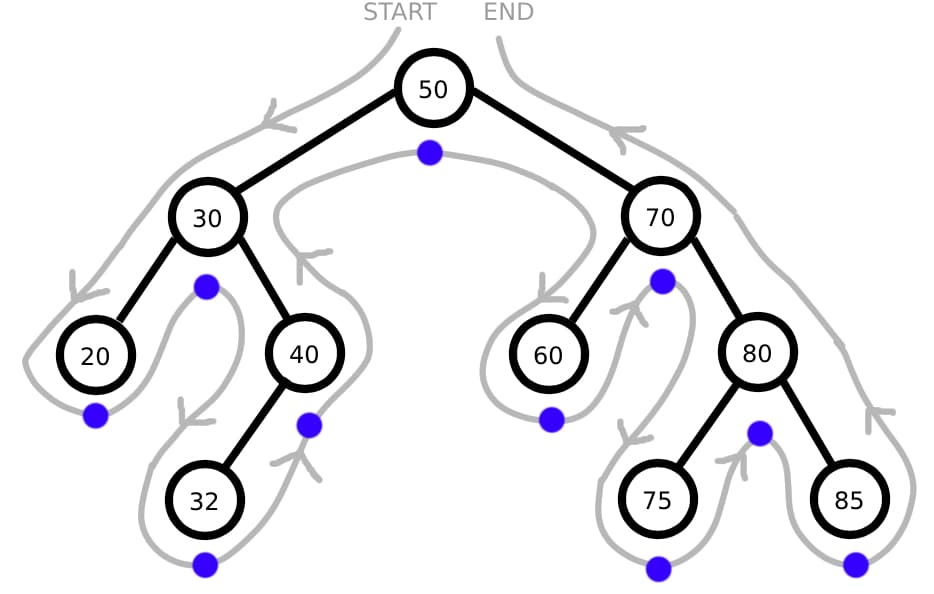
The order we pass through the spots this time gives the sequence: 20, 30, 32, 40, 50, 60, 70, 75, 80, 85. This is the in-order traversal of the tree.
Finally, placing the spot on the right of each node will give the post-order traversal:
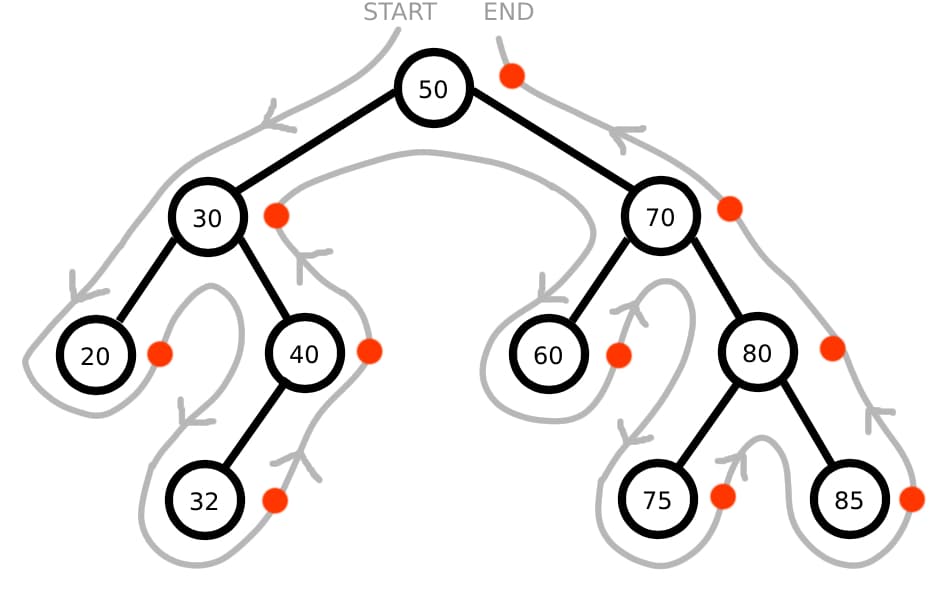
This time the sequence is: 20, 32, 40, 30, 60, 75, 85, 80, 70, 50.
This is a useful method for figuring out visually how each method traverses the tree. Now let’s look at coding them!
Pre-Order Traversal
If we think about how we want the code to work, a recursive solution appears the most natural. On each subtree we come to, we want to first visit the root, then the left child, then the right child. If one of the children is not a leaf (ie. it has its own children), we recursively call again with this child as the new root.
So code for this traversal could be as follows:
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = None
def insertChild(self, node, value):
if node is None:
return Tree(value)
if value < node.value:
node.leftChild = self.insertChild(node.leftChild, value)
elif value > node.value:
node.rightChild = self.insertChild(node.rightChild, value)
return node
def preOrderTraversal (self, root):
if root is not None:
print(root.value)
self.preOrderTraversal(root.leftChild)
self.preOrderTraversal(root.rightChild)
else:
returnNote that the initial quick summary I gave that describes the order the traversals visit nodes is more useful for implementation than the section on visualisation. For pre-order, if the node is not ‘None’, we know to first visit the root, then the left, then the right. This is performed in the if-statement. Otherwise, if the root is none, the recursion ends and the function just returns ‘None’.
So let’s build our tree again, and see what this function prints.
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = None
def insertChild(self, node, value):
if node is None:
return Tree(value)
if value < node.value:
node.leftChild = self.insertChild(node.leftChild, value)
elif value > node.value:
node.rightChild = self.insertChild(node.rightChild, value)
return node
def preOrderTraversal (self, root):
if root is not None:
print(root.value)
self.preOrderTraversal(root.leftChild)
self.preOrderTraversal(root.rightChild)
else:
return
if __name__ == '__main__':
rootNode = Tree(50)
rootNode.insertChild(rootNode, 30)
rootNode.insertChild(rootNode, 20)
rootNode.insertChild(rootNode, 40)
rootNode.insertChild(rootNode, 32)
rootNode.insertChild(rootNode, 70)
rootNode.insertChild(rootNode, 60)
rootNode.insertChild(rootNode, 80)
rootNode.insertChild(rootNode, 75)
rootNode.insertChild(rootNode, 85)
rootNode.preOrderTraversal(rootNode)
This matches what we found when we visualised the traversal by hand!
This is the only traversal method that visits parents before it visits children. Hence it is best used for cloning a given tree. If we are trying to clone a tree, we need each parent to exist first before we can give it children. This traversal allows us to visit the parent first so is the best choice for this use case.
In-Order Traversal
Our code solution here will be incredibly similar to what we’ve written for pre-order traversal. The only difference is that for each subtree we want to now visit the left child first, then the root, then the right child. All we need to change is the order of the statements in the if-statement:
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = None
def insertChild(self, node, value):
if node is None:
return Tree(value)
if value < node.value:
node.leftChild = self.insertChild(node.leftChild, value)
elif value > node.value:
node.rightChild = self.insertChild(node.rightChild, value)
return node
def inOrderTraversal (self, root):
if root is not None:
self.inOrderTraversal(root.leftChild)
print(root.value)
self.inOrderTraversal(root.rightChild)
else:
returnAs we can see the code now reflects this new order for visiting nodes. Applied to our example tree in the same way as before, it prints:
Again it matches our manual attempt to create the sequence.
For a binary search tree, In-order traversal will always print out the elements in non-decreasing order. This is useful for fairly obvious reasons – we tend to like it when things are sorted! If we wanted a non-increasing order of elements we could modify the code to visit the right child, then the root, then the left child.
Post-Order Traversal
As before, only a minor modification to the code is required to implement a post-order traversal. We simply reorder the statements so that we visit the left child first, then the right child, then the root.
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = None
def insertChild(self, node, value):
if node is None:
return Tree(value)
if value < node.value:
node.leftChild = self.insertChild(node.leftChild, value)
elif value > node.value:
node.rightChild = self.insertChild(node.rightChild, value)
return node
def postOrderTraversal (self, root):
if root is not None:
self.postOrderTraversal(root.leftChild)
self.postOrderTraversal(root.rightChild)
print(root.value)
else:
returnApplied to our example tree, it prints:
Looks correct again!
Post order visits all the children before it visits their parent node. This makes it a really good choice for deleting a binary tree. When we delete, we clearly want to first remove the children before the parent and this let’s us do that.
Breadth-First Traversal
We’ve had a good look at depth-first traversal methods so now we can turn our attention to the other main way of traversing a tree: breadth-first. This isn’t separated into three subcategories like before; breadth-first traversal exists on its own.
The key here is to visit every node at a particular level of the tree before moving on to the next level. By ‘level’ I’m referring to all the nodes that are at the same distance from the root. Let’s look at our example tree again to see this:
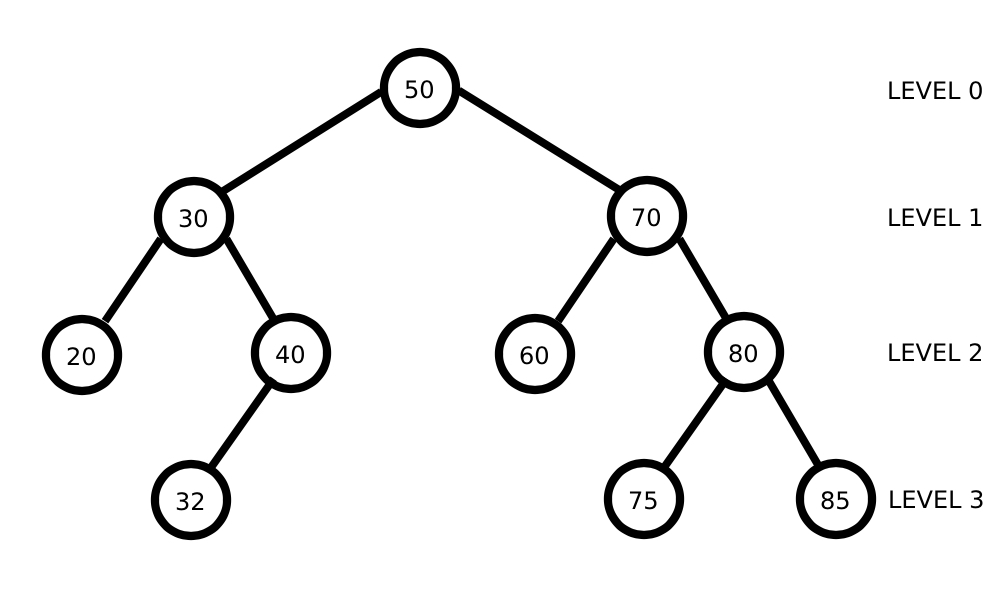
So initially we’ll print 50. Then we’ll print 30, 70. Then we’ll print 20, 40, 60, 80. Finally, we’ll print 32, 75, 85.
For the code, I think the easiest way to implement it will be using a queue data structure. For those unfamiliar, it works exactly the same as a queue in the real world. Items can only join the queue at the back, and leave from the front. That’s really all there is to it.
So when we’re on a particular level of the tree, for each node we encounter we will print it’s value and then add it’s children to a queue. This will build a complete queue holding all the children of the current level. We then recursively call the function on each child in the queue (removing the child from the queue as we do this) until it’s empty. Here is an implementation of the breadth-first traversal.
from queue import Queue
queue = Queue()
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = None
def insertChild(self, node, value):
if node is None:
return Tree(value)
if value < node.value:
node.leftChild = self.insertChild(node.leftChild, value)
elif value > node.value:
node.rightChild = self.insertChild(node.rightChild, value)
return node
def breadthFirstTraversal (self):
print(self.value)
if self.leftChild is not None:
queue.put(self.leftChild)
if self.rightChild is not None:
queue.put(self.rightChild)
while queue.empty() is False:
queue.get().breadthFirstTraversal()
if __name__ == '__main__':
rootNode = Tree(50)
rootNode.insertChild(rootNode, 30)
rootNode.insertChild(rootNode, 20)
rootNode.insertChild(rootNode, 40)
rootNode.insertChild(rootNode, 32)
rootNode.insertChild(rootNode, 70)
rootNode.insertChild(rootNode, 60)
rootNode.insertChild(rootNode, 80)
rootNode.insertChild(rootNode, 75)
rootNode.insertChild(rootNode, 85)
rootNode.breadthFirstTraversal()First note that I have imported a Python implementation of a queue. Second, our exit condition for ending the recursion is a little more subtle because there’s no return statements here (in Python, leaving no return statement will implicitly return ‘None’). We only add children to the queue if they pass the if-statement, ie. the child is not ‘None’. At the bottom of the tree all the children will be ‘None’ so nothing will be added to the queue. This means the while-loop will terminate immediately because the queue is empty, ending the recursion.
This code outputs:
This is consistent with what I said it should be! Our implementation seems correct.
One quick note to bear in mind is that breadth-first traversal uses much more memory than depth-first because you have to store all the nodes at the level that you’re on. For us this is okay but for enormous trees with multiple orders of magnitude more nodes per level it might become a concern. A solution for this circumstance could be to parallelise the algorithm over distributed-memory machines, but we will not go into that here.
Uses for this could be for finding people of a particular generation in a family tree, or returning files at a given level in a directory.
Finding the Height of a Tree
We’ve covered all the standard methods of traversing a tree which is the main goal I wanted to achieve, however if you’re interested in getting a little more exposure to trees I’m going to carry on adding a few extra methods to our class. The first will be finding the height of the tree. As a reminder the height is the longest path from the root to a leaf. It is equivalent to the number of levels we have in the tree. From the figure above we can see that there are four levels in the tree so the height of this tree is four.
The algorithm once again lends itself to a recursive implementation. At each node we can call the function again on both of its children. We terminate the recursion when we reach a leaf (ie. no further children exist). As we work back up the recursive stack, we’re clearly only interested in the child that gave us the largest depth to a leaf so we take the maximum value out of the left depth and the right depth. Then we need to also increment by one to account for the root node we are starting from.
Here is a possible implementation.
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = None
def insertChild(self, node, value):
if node is None:
return Tree(value)
if value < node.value:
node.leftChild = self.insertChild(node.leftChild, value)
elif value > node.value:
node.rightChild = self.insertChild(node.rightChild, value)
return node
def calculateHeight(self, node):
if node is None:
return 0
else:
leftDepth = self.calculateHeight(node.leftChild)
rightDepth = self.calculateHeight(node.rightChild)
return max(leftDepth, rightDepth) + 1Our exit condition is of course the case when no further children exist, meaning we are at a leaf so we just return 0 (the distance from a leaf to itself is 0).
Let’s check this on our example tree:
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = None
def insertChild(self, node, value):
if node is None:
return Tree(value)
if value < node.value:
node.leftChild = self.insertChild(node.leftChild, value)
elif value > node.value:
node.rightChild = self.insertChild(node.rightChild, value)
return node
def calculateHeight(self, node):
if node is None:
return 0
else:
leftDepth = self.calculateHeight(node.leftChild)
rightDepth = self.calculateHeight(node.rightChild)
return max(leftDepth, rightDepth) + 1
if __name__ == '__main__':
rootNode = Tree(50)
rootNode.insertChild(rootNode, 30)
rootNode.insertChild(rootNode, 20)
rootNode.insertChild(rootNode, 40)
rootNode.insertChild(rootNode, 32)
rootNode.insertChild(rootNode, 70)
rootNode.insertChild(rootNode, 60)
rootNode.insertChild(rootNode, 80)
rootNode.insertChild(rootNode, 75)
rootNode.insertChild(rootNode, 85)
print(rootNode.calculateHeight(rootNode))Outputs:
As expected!
Summing Along the Path from the Root to a Leaf
This is an interesting problem to end on because it requires a couple of different ideas to make it work. It’s not too difficult though! Basically we want to allow the user to input a number and, if that number exists as a leaf in the tree, then we will output the sum of all the nodes we pass through on a path from the root to that leaf. We will incorporate some error handling to make sure the number entered is a leaf in the tree.
To start with, we’ll make the function for summing along the path to the leaf. It will be a recursive solution once again and we’ll exploit the main property of the binary search tree. That is to say, we can easily navigate to the required leaf by checking whether the leaf’s value is greater than or less than the node we are currently at. As an example, if the leaf’s value is greater than that of the current node, we’ll recursively call the function again on the right child of the current node. This approach will continue down to the target leaf which will simply return its own value.
Here is the implementation:
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = None
def insertChild(self, node, value):
if node is None:
return Tree(value)
if value < node.value:
node.leftChild = self.insertChild(node.leftChild, value)
elif value > node.value:
node.rightChild = self.insertChild(node.rightChild, value)
return node
def rootToLeafSum (self, node, leaf):
totalSum = node.value
if node.value == leaf:
return leaf
elif leaf < node.value:
totalSum += self.rootToLeafSum(node.leftChild, leaf)
elif leaf > node.value:
totalSum += self.rootToLeafSum(node.rightChild, leaf)
return totalSumAs a reminder, here is our tree:
So lets test the code, inputting the leaf as 75.
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = None
def insertChild(self, node, value):
if node is None:
return Tree(value)
if value < node.value:
node.leftChild = self.insertChild(node.leftChild, value)
elif value > node.value:
node.rightChild = self.insertChild(node.rightChild, value)
return node
def rootToLeafSum (self, node, leaf):
totalSum = node.value
if node.value == leaf:
return leaf
elif leaf < node.value:
totalSum += self.rootToLeafSum(node.leftChild, leaf)
elif leaf > node.value:
totalSum += self.rootToLeafSum(node.rightChild, leaf)
return totalSum
if __name__ == '__main__':
rootNode = Tree(50)
rootNode.insertChild(rootNode, 30)
rootNode.insertChild(rootNode, 20)
rootNode.insertChild(rootNode, 40)
rootNode.insertChild(rootNode, 32)
rootNode.insertChild(rootNode, 70)
rootNode.insertChild(rootNode, 60)
rootNode.insertChild(rootNode, 80)
rootNode.insertChild(rootNode, 75)
rootNode.insertChild(rootNode, 85)
print(rootNode.rootToLeafSum(rootNode, 75))This outputs:
Since 75 + 80 + 70 + 50 = 275, this output seems correct!
But error checking is a very important part of this implementation because if the leaf we input isn’t actually a leaf in the tree then our recursion will never terminate. To handle error checking, we need to generate a list holding all the leaves and then check the user’s input against this list.
The function to produce the list of leaves will borrow very similar ideas from other functions we’ve created so far. Given a node in the tree, we will recursively call the function on its children and continue doing this until both of a node’s children are ‘None’. Then we will add this node to our list of leaves.
Here is the code:
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = None
def insertChild(self, node, value):
if node is None:
return Tree(value)
if value < node.value:
node.leftChild = self.insertChild(node.leftChild, value)
elif value > node.value:
node.rightChild = self.insertChild(node.rightChild, value)
return node
def findLeaves(self, node):
leaves = []
if node is None:
return []
elif (node.leftChild == None) & (node.rightChild == None):
leaves.append(node.value)
else:
leaves = leaves + self.findLeaves(node.leftChild)
leaves = leaves + self.findLeaves(node.rightChild)
return leaves
if __name__ == '__main__':
rootNode = Tree(50)
rootNode.insertChild(rootNode, 30)
rootNode.insertChild(rootNode, 20)
rootNode.insertChild(rootNode, 40)
rootNode.insertChild(rootNode, 32)
rootNode.insertChild(rootNode, 70)
rootNode.insertChild(rootNode, 60)
rootNode.insertChild(rootNode, 80)
rootNode.insertChild(rootNode, 75)
rootNode.insertChild(rootNode, 85)
print(rootNode.findLeaves(rootNode))This outputs:
Referring to the above image of our tree, we can confirm that this is a correct list of leaves.
So now before we try to sum along the path to the given leaf, we’ll just quickly check that that leaf is valid. I’ve added a new class to handle the exception and also added some extra code to continue asking the user for a number until they give a valid one.
Here is everything all together:
class LeafNotInTreeError(Exception):
pass
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = None
def insertChild(self, node, value):
if node is None:
return Tree(value)
if value < node.value:
node.leftChild = self.insertChild(node.leftChild, value)
elif value > node.value:
node.rightChild = self.insertChild(node.rightChild, value)
return node
def rootToLeafSum (self, node, leaf):
totalSum = node.value
if node.value == leaf:
return leaf
elif leaf < node.value:
totalSum += self.rootToLeafSum(node.leftChild, leaf)
elif leaf > node.value:
totalSum += self.rootToLeafSum(node.rightChild, leaf)
return totalSum
def findLeaves(self, node):
leaves = []
if node is None:
return []
elif (node.leftChild == None) & (node.rightChild == None):
leaves.append(node.value)
else:
leaves = leaves + self.findLeaves(node.leftChild)
leaves = leaves + self.findLeaves(node.rightChild)
return leaves
if __name__ == '__main__':
rootNode = Tree(50)
rootNode.insertChild(rootNode, 30)
rootNode.insertChild(rootNode, 20)
rootNode.insertChild(rootNode, 40)
rootNode.insertChild(rootNode, 32)
rootNode.insertChild(rootNode, 70)
rootNode.insertChild(rootNode, 60)
rootNode.insertChild(rootNode, 80)
rootNode.insertChild(rootNode, 75)
rootNode.insertChild(rootNode, 85)
treeLeaves = rootNode.findLeaves(rootNode)
while True:
try:
leaf = int(input("Enter a leaf: "))
if leaf not in treeLeaves:
raise LeafNotInTreeError()
break
except LeafNotInTreeError:
print("That leaf doesn't exist in the tree!")
except Exception as e:
print("Please enter an integer")
print("The sum from the root to %d is: %d" % (leaf, rootNode.rootToLeafSum(rootNode, leaf)))I will first input a string, then a float, then an integer that isn’t a leaf. This will check the error handling. I will then enter a valid leaf to check if the sum works. Here is the output code from this testing:
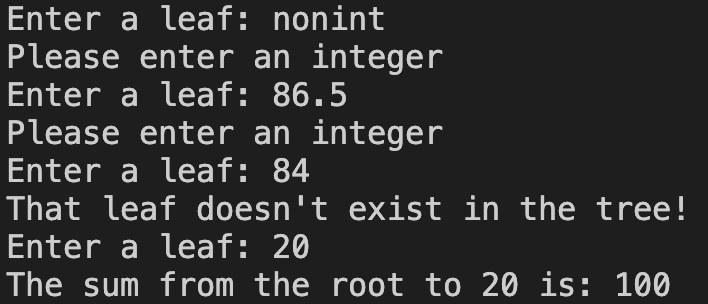
Everything has worked as intended, including the sum to the leaf with value 20!
Summary
I will leave all the code for the entire class here, along with the code to form the tree we have been using as an example throughout.
from queue import Queue
queue = Queue()
class LeafNotInTreeError(Exception):
pass
class Tree:
def __init__(self, value):
self.value = value
self.leftChild = None
self.rightChild = None
def insertChild(self, node, value):
if node is None:
return Tree(value)
if value < node.value:
node.leftChild = self.insertChild(node.leftChild, value)
elif value > node.value:
node.rightChild = self.insertChild(node.rightChild, value)
return node
def inOrderTraversal (self, root):
if root is not None:
self.inOrderTraversal(root.leftChild)
print(root.value)
self.inOrderTraversal(root.rightChild)
else:
return
def preOrderTraversal (self, root):
if root is not None:
print(root.value)
self.preOrderTraversal(root.leftChild)
self.preOrderTraversal(root.rightChild)
else:
return
def postOrderTraversal (self, root):
if root is not None:
self.postOrderTraversal(root.leftChild)
self.postOrderTraversal(root.rightChild)
print(root.value)
else:
return
def breadthFirstTraversal (self):
print(self.value)
if self.leftChild is not None:
queue.put(self.leftChild)
if self.rightChild is not None:
queue.put(self.rightChild)
while queue.empty() is False:
queue.get().breadthFirstTraversal()
def calculateHeight(self, node):
if node is None:
return 0
else:
leftDepth = self.calculateHeight(node.leftChild)
rightDepth = self.calculateHeight(node.rightChild)
return max(leftDepth, rightDepth) + 1
def rootToLeafSum (self, node, leaf):
totalSum = node.value
if node.value == leaf:
return leaf
elif leaf < node.value:
totalSum += self.rootToLeafSum(node.leftChild, leaf)
elif leaf > node.value:
totalSum += self.rootToLeafSum(node.rightChild, leaf)
return totalSum
def findLeaves(self, node):
leaves = []
if node is None:
return []
elif (node.leftChild == None) & (node.rightChild == None):
leaves.append(node.value)
else:
leaves = leaves + self.findLeaves(node.leftChild)
leaves = leaves + self.findLeaves(node.rightChild)
return leaves
if __name__ == '__main__':
rootNode = Tree(50)
rootNode.insertChild(rootNode, 30)
rootNode.insertChild(rootNode, 20)
rootNode.insertChild(rootNode, 40)
rootNode.insertChild(rootNode, 32)
rootNode.insertChild(rootNode, 70)
rootNode.insertChild(rootNode, 60)
rootNode.insertChild(rootNode, 80)
rootNode.insertChild(rootNode, 75)
rootNode.insertChild(rootNode, 85)So today we’ve explored how to make a basic tree in Python, how to traverse it in multiple ways, and covered some extra functions on the tree!
Some possible extensions for you to implement yourself could be:
- Return all the children on just one particular level of the tree. - Given a number, return true if there exists a path from root to a leaf that sums to this number. False otherwise. - Create the equivalent of this class for a tree with arbitrarily many children per node.
You can also download this code from GitHub here. I hope you’ve enjoyed learning about trees!